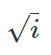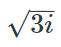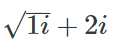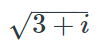Create accessible math in Pressbooks and Canvas
On this page:
- Overview
- Encode accessible math in Pressbooks
- Encode accessible math in Canvas
- Make math accessible in Canvas Classic Quizzes and Quick Checks
Overview
To make math equally accessible to all students, you need to provide math in a digital form that can be read with a screen reader, just like with text. You can do this easily in both Pressbooks and Canvas. The gold standard for providing accessible math is using MathML and MathJax to produce a navigable and scalable math object.
A student equipped with a screen reader or braille display should be able to navigate any single-line math reasonably easily. If possible, expand equations with multiple cases so that each case appears as a separate equation on its own. If, as an instructor, you have received a course accommodation request, you will likely need to convert matrices and complex tables to braille. Fortunately, math that is screen-reader accessible will not require any further modifications before being submitted for braille conversion.
Encode accessible math in Pressbooks
Pressbooks is a tool that enables faculty and students at IU to create and publish text in multiple formats. Although Pressbooks does not have an equation editor for inserting math, it does give users the ability to quickly insert LaTeX with appropriate delimiters and, like Canvas, it will render any LaTeX using MathJax upon saving. Pressbooks also gives users options related to which delimiters are used. For more, see Adding Mathematical Notation.
Encode accessible math in Canvas
Upon loading, Canvas pages are checked for LaTeX code or equation editor objects. If any LaTeX code or equation editor objects are discovered, MathJax will convert them into accessible math objects. To encode your math, use the equation editor, or:
- Navigate to the Canvas page, quiz, assignment, etc. where you want to insert math.
- At the upper-right, select .
- Wherever you have or want to have math (for example, "a x b = 4"):
- Write it out using LaTeX (for example,
a \times b = 4). - If you want the math to be on its own line, put
\[and\]on either side (for example,\[ a \times b = 4 \]).If you want the math to be inline, put
\(and\)on either side (for example,\( a \times b = 4 \)).
- Write it out using LaTeX (for example,
- Save. You should now see the math render from its LaTeX form into its visual and accessible MathML form.
Make math accessible in Canvas Classic Quizzes and Quick Checks
Unfortunately, because of the way browsers currently handle math and the way that HTML form elements have been designed, any math rendered with MathJax or straight MathML code that is included in the label of a form control (such as a radio button) will not be correctly conveyed to screen-reading software or other assistive technologies. This means that any LaTeX or equation editor objects placed in the answer options of a Canvas quiz or Quick Check multiple choice question (since they become radio button labels) will not produce accessible math. This limitation is not dependent on the user's hardware, screen-reading software, or browser.
Recommended workaround 1
Provide the answer options in the question area, using LaTeX code for the math and labels that correspond to labels in the answer selection area. This allows for the math in the answer options to be explorable.
For example:
Question area:
What is \(\sqrt{1i+2i}\)?
- \(\sqrt{i}\)
- \(\sqrt{3i}\)
- \(\sqrt{1i}+2i\)
- \(\sqrt{3+i}\)
Answer selection area:
- A
- B
- C
- D
Recommended workaround 2
Keep the math inside the answer selection area, but express the math in words using MathSpeak grammar. MathSpeak is often straightforward enough to pose no problem for sighted students, but to avoid any confusion, the best practice is to provide an image of the mathematics and set the image's alt-text to the math's MathSpeak equivalent. This allows the math to be viewed in the area where it will need to be selected, but it does not allow the math of the answer options to be explored.
For example:
Question area:
What is \(\sqrt{1i+2i}\)?
Answer selection area:
This is document bgkz in the Knowledge Base.
Last modified on 2024-05-29 09:43:43.